Basic properties of springs

When designing a spring, the following basic performance characteristics should be considered: ① the spring's characteristic curve, i.e., the relationship between load and deformation; ② the spring's strain energy; ③ the spring's natural frequency; ④ the amplitude of the spring under forced vibration. These characteristics are briefly described below.

1.1 Characteristic curve and stiffness of a spring

The curve relating load F (or T) to deformation f (or φ) is called the characteristic curve of a spring, as shown in Figure 1-1. There are roughly three types of characteristic curves for springs:

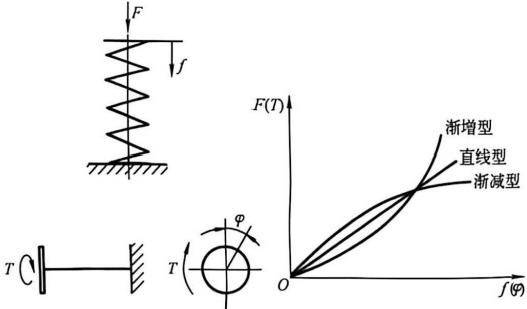
Figure 1-1 Characteristic curve of a spring

① Linear; ② Gradually increasing; ③ Gradually decreasing. Some springs exhibit characteristic curves that can be a combination of two or three of these types (Figure 1-2), known as combined characteristic curves. For example, the characteristic curve of a truncated cone spiral spring (Figure 1-2a) is linear at the beginning of loading, but becomes gradually increasing after a certain degree of deformation; the characteristic curve of a disc spring (Figure 1-2b) is initially gradually decreasing, then gradually increasing, with the entire characteristic curve forming an S-shape; and the characteristic curve of a ring spring (Figure 1-2c) is linear under loading, but gradually increasing under unloading.A combined characteristic curve can also be obtained using a combination of springs, as shown in Figure 1-2d, which illustrates the characteristic curves of two parallel combined helical springs at different heights. Initially, only one spring bears the load, so the characteristic curve represents only the load-bearing spring. As the loaded spring deforms to a certain extent under load, the other spring also begins to bear the load. At this point, the characteristic curve transforms into a curve representing the combined load of both springs, and thus its slope changes.

The ratio of the load increment dF (or dT) to the deformation increment df (or dφ), i.e., the load required to produce a unit deformation, is called the stiffness of the spring. For compression and tension springs, the stiffness is

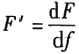                                                              (1-1a)

For the stiffness of the torsion spring is

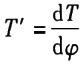                                                             (1-2a)

A spring with a gradually increasing characteristic curve has a stiffness that increases with increasing load; while a spring with a gradually decreasing characteristic curve has a stiffness that decreases with increasing load. A straight spring, however, has a stiffness that does not change with the load.

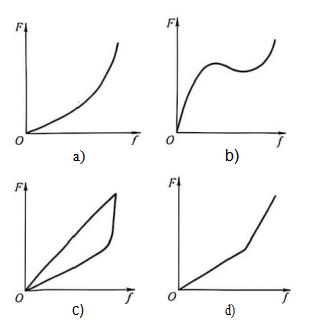
Figure 1-2 Combined Characteristic Lines

a) Frustum spiral spring

b) Disc spring

c) Circular spring

d) Combined spring

Therefore, for a spring with a linear characteristic curve, its stiffness is also called the spring constant.

The deformation of a spring caused by a unit force, which is the reciprocal of its stiffness, is called the spring's flexibility.

The characteristic curve of a spring plays a guiding role in the design and selection of spring types. As shown in Figure 1-2a, the characteristic curve of a truncated conical spiral spring shows that the spring stiffness increases sharply when the load reaches a certain level. Due to this characteristic, when the spring is subjected to excessive load, the increase in spring deformation is relatively small, thus protecting the spring. Therefore, springs with this characteristic curve are suitable for situations with limited space and large loads. For example, an air spring with a height control valve has an S-shaped characteristic curve as shown in Figure 1-2b, which is the ideal state for a vehicle suspension system. This is because the stiffness is relatively low in the middle section of this curve, while the stiffness gradually increases in the final section of the extension and compression stroke. This ensures that the vehicle is very soft during normal operation, but gradually stiffens when the air spring is significantly stretched and compressed when passing over rough roads, thus limiting the amplitude of vehicle body vibration. Figure 1-2c shows the characteristic curve of a ring compression spring or leaf spring, indicating that the spring consumes some frictional work, or absorbs some energy, during loading and unloading. Therefore, springs with this type of characteristic curve are suitable for vibration damping and cushioning.

When designing springs, their characteristic curves can be calculated using analytical methods. However, even the most accurate and meticulous calculations will always differ to some extent from the actual values. This is due to the unavoidable manufacturing errors in the springs and the non-uniformity of the material structure. Therefore, when designing springs, to ensure the required characteristic curve, it is necessary to conduct experiments and repeatedly modify relevant dimensions to finally achieve the desired characteristic curve.

When designing springs with nonlinear characteristic curves, static deformation must sometimes be considered. As shown in Figure 1-3, static deformation refers to the deformation f, the distance between the point of tangency (a) and the projection of point a onto the horizontal coordinate axis, when a tangent line is drawn through any point a on the characteristic curve. This distance is called the static deformation of the load F₅ corresponding to the point a.

www.raleigh-springs.com
Raleigh Spring Technology Co., Ltd.

About Author

admin

See author's posts